Melchizedek Foren-Archiv 22.08.08 - 05.11.11Willenswissenschaftweise Magie rechter Beziehung "Ich bin der Schöpfer meiner eigenen Wirklichkeit!" Gruppenbewusstsein Kuthumi 12 Strahlen ● Mahatma 11:11 Kirche ● Kommentar Archiv 2004 - 2008 (Verzeichnis ohne Index, als Zip-Datei) www.melchizedek-forum.de geschrieben von Lhatara am 12.05.2009 um 20:52:48 - als Antwort auf: Nachbereitung Rudra-Gruppe vom 2. Mai von Bhairava >Königsberg an das Deutsche Reich zurückgeben: >dann wird B. Obamas âAtombomben wegâ möglich * Das Königsberger Brückenproblem Zur Zeit von Leonard Euler floà in Königsberg der Fluà Pregel zusammen. Euler stellte sich die folgende Frage: Ist es möglich, alle Brücken nacheinander zu passieren, ohne eine auszulassen oder mehr als einmal zu überschreiten? Das Problem ist nicht gerade ein Optimierungsproblem, man könnte es zur Not vielleicht in die Kategorie Problem des kürzesten Weges pressen. Es gibt eine Spezialbezeichnung für die Klasse solcher Probleme: Zeichnen eines Bildes in einem Zug. Tiefgehender beschäftigt sich die Topologie mit derartigen Aufgaben. Euler zeigte, dass das vorliegende Problem nicht lösbar ist, er formulierte sogar eine allgemeine notwendige und hinreichende Bedingung: Ein Bild ist in einem Zug zeichenbar, wenn es entweder genau zwei oder keinen Knotenpunkt ungeraden Grades besitzt. Als Knotenpunkte ungeraden Grades sind all jene Knoten eines ungerichteten Graphen zu verstehen, die eine ungerade Anzahl benachbarter Kanten besitzen. Betrachten wir den Graphen des vorliegenden Problems in der Abbildung 5.rechts, ist leicht zu erkennen, dass tatsächlich die notwendige Bedingung nicht erfüllt ist. 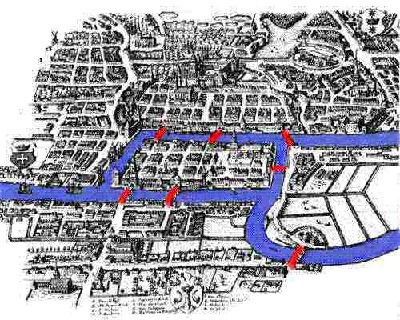 Antworten zu diesem Beitrag: |